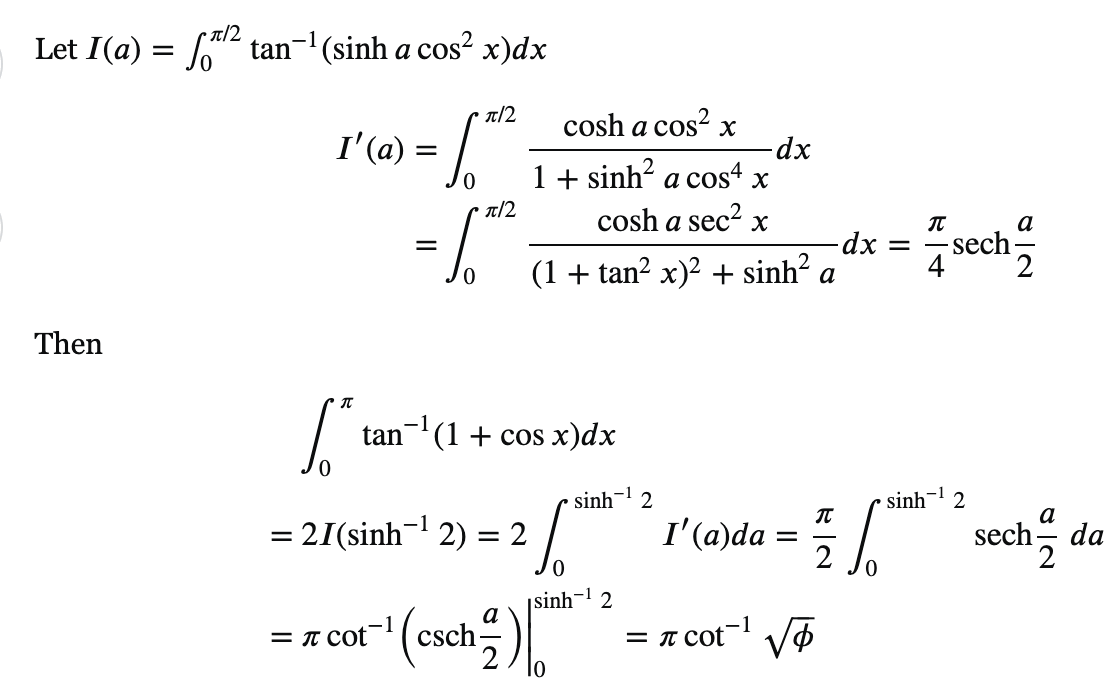Happy #PiDay! Pretty cool to have a blood moon total lunar eclipse overnight as we entered Pi Day 2025. Plenty of circles and spheres to celebrate on this last day of winter quarter classes. Cheers!
Having fun playing with my new wooden soma cube. Don't know why I didn't know this before, but it can be rearranged from 3x3x3 to 4x4x2 minus 5 contiguous unit cubes that form the shape of a pentomino (1 deep). 11 of the pentominos work (of the 12). Way cool!
https://www.youtube.com/watch?v=dGSHMhLCLLM
How mathematics built the modern world: Mathematics was the cornerstone of the Industrial Revolution. A new paradigm of measurement and calculation, more than scientific discovery, built industry, modernity, and the world we inhabit today.
Long read article from late 2023, I'm so behind on my "to read" list. Interesting history and perspectives of mathematics. Recommended by a recent guest on #EzraKlein podcast.
https://worksinprogress.co/issue/how-mathematics-built-the-modern-world/
"Most of the significant inventions of the Industrial Revolution were not undergirded by a deep scientific understanding, and their inventors were not scientists."
"The standard chronology ignores many of the important events of the previous 500 years. Widespread trade expanded throughout Europe. Artists began using linear perspective and mathematicians learned to use derivatives. Financiers started joint stock corporations and ships navigated the open seas. Fiscally powerful states were conducting warfare on a global scale."
"There is an intellectual thread that runs through all of these advances: measurement and calculation."
Image: Water wheel from Ramelli’s Le Diverse et Artificiose Machine (1588).
#MAA's Math Values blog is asking for Pi-ku submissions for Pi Day (March 14). We all know a haiku is a Japanese poem that (very simplified) consists of three lines with syllable count for each line being 5-7-5.
A Pi-ku is also a poem consisting of three lines, but this time the syllables count for each line is 3-1-4 respectively. For instance:
I really
Love
Mathematics!
Math Values writes, "In celebration of Pi Day, we invite our readers to try writing your own Pi-kus. They can overtly be about math, or subtly about math, or not about math at all. Email your Pi-kus to blogs@maa.org by March 3, 2025, and we'll compile them into a community-wide celebratory post for Pi Day."
Curiosity is key to scientific and mathematical discoveries and understanding. New video from Sanderson / 3Blue1Brown connects light and waves and colours and more. Fun watch!
Attn new winter quarter Calculus students: Notice the vectors, curves, and direction of movement? We'll learn more this term especially in Calc III :)
The barber pole optical mystery: https://www.youtube.com/watch?v=0TdBP9m4R74
#HigherEducation faculty play an essential role in educating for a #democracy. Colleges and universities should not be "repositories of knowledge but also catalysts for social change."
Article in today's Inside Higher Ed: https://www.insidehighered.com/news/institutions/2024/11/15/report-offers-playbook-higher-eds-role-democracy
Complete College, America (CCA), announcement of their new white paper: https://completecollege.org/resource/complete-college-america/
Executive Summary: https://completecollegeamerica.s3.us-east-2.amazonaws.com/wp-content/uploads/2024/11/13211742/CompleteCollegeAmerica-RenewDemocracy-summary.pdf
Gather4Gardner.org (#MartinGardner) has been busy loading videos from their G4G15 conference earlier this year. Check them out at https://www.youtube.com/playlist?list=PL5_D5QQxvWKUPpMY3eNV-PrIzh1uHlR8x One of my faves is the Mesmoid. Calculus students >> check out the graphs and diagrams at about the 3:40 mark. https://www.youtube.com/watch?v=_KU6JdikGK4
What's the probability that two students in a class of 23 have a birthday on the same day? Surprising over 50%!! Three famous mathematical paxadoxes from Sci Am: Hilbert’s Hotel, Birthday Paradox, and Russell’s Antinomy. https://www.scientificamerican.com/article/three-of-the-strangest-paradoxes-in-mathematics
Teaching a #calculus III course this fall that includes sequences and #series. In resources, I typically (externally) link to three different "flowcharts" that each asks yes/no Qs that students use to help them decide which #SeriesTest would work in determining if a series is #convergent or #divergent (example below).
However, the three I typically share don't pass accessibility standards (tagged PDF, headers, colour contrast, etc). I hate to recommend them if they aren't an #accessible document. Does anyone happen to have online a Series Test Flowchart that is accessible?
"...possible breakthrough in a very old, very sticky problem in number theory. #RiemannsHypothesis —concerning the distribution of prime numbers throughout the number line — dates back over 160 years. While the new paper doesn’t purport to solve the problem, it could be a substantial step toward a solution. That could enable other number theorists to keep taking steps toward solving it, and (perhaps more importantly) winning a $1 million prize." https://www.popularmechanics.com/science/math/a61491065/mathematicians-close-to-solving-notorious-math-problem-riemann-hypothesis/ The seven #MillenniumProblems: https://www.claymath.org/millennium-problems/
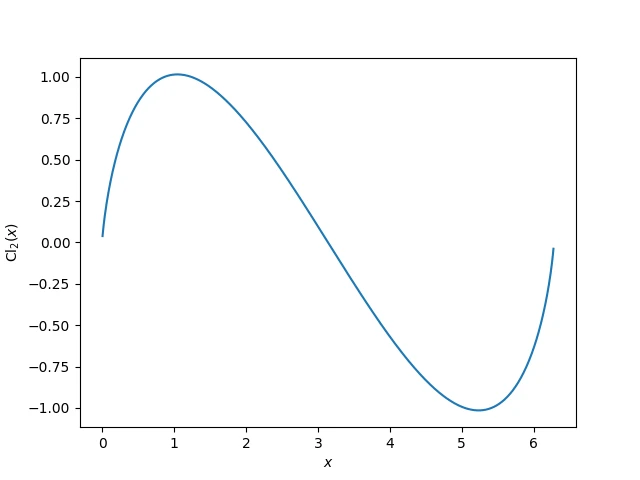
Fundamental Theorem of Calculus lovers read this! "The Clausen function can be defined in terms of its Fourier series" https://www.johndcook.com/blog/2024/07/01/the-clausen-function/
Attn Calc II students: Saw this integral on Stack Exchange today: \( \int_{0}^{2\pi}\sin(x)\sin(2x)\sin(3x)\sin(4x)\ dx=\frac{\pi}{4} \) Wolfram Alpha confirms https://www.wolframalpha.com/input?i=int_0%5E%282pi%29+%28sin%28x%29+sin%282x%29+sin%283x%29+sin%284x%29%29+dx So can it be generalized? Yes! Find integral over [0,2pi] of the product of sin(kx), k=1 to n. Discuss in class! (Or over dinner ;-)
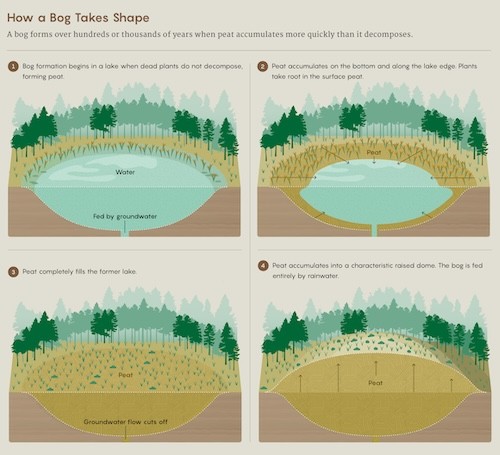
"Bogs and other peatlands occupy around 3% of Earth’s land. Yet they manage to pack away twice as much carbon as all the planet’s trees. If that carbon were released, atmospheric carbon dioxide would double, with potentially disastrous consequences for humans and many other species."
Mathematicians took on the task of modeling the size/shape of bogs to get good estimates of the potential dangers.
"The bog’s shape seemed to be essentially governed by the physics of the water table. The researchers found that they could mathematically model the shape of the bog by solving a widely used equation named for the 19th-century mathematician Siméon-Denis Poisson that allowed them to approximate a bog’s depth given only the shape of its boundary."
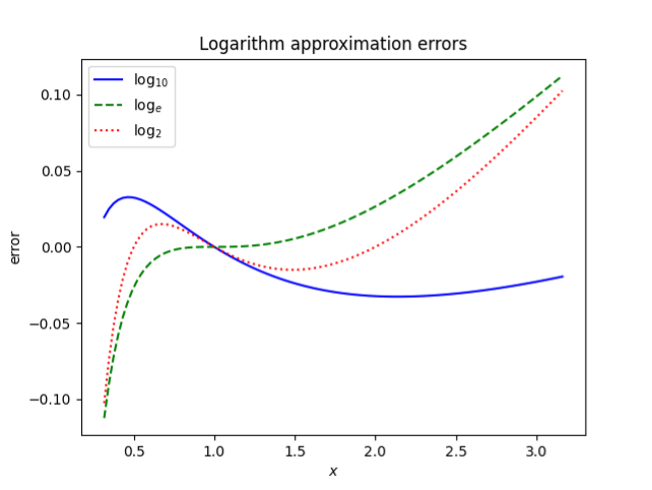
Attn College Algebra students. ln(x) can be approximated by 2(x-1)/(x+1) and log(x) can be approximated by (x-1)/(x+1). (Try some x-values!) And yet ln(x) is not twice log(x). What's going on here? John D. Cook has useful information about the approximation error here. Watch the scale on the graphs provided. https://www.johndcook.com/blog/2024/05/12/logarithm-approximation-error/ Image source: John D. Cook
RIP Jim Simons. Mathematician, Billionaire, Philanthropist. He will be missed.
Here Jim provides a short story of his life in mathematics at Abel Prize week in 2022. "I made a lot of money and gave it all away." "I was lucky enough to solve the problem through ambient dimension 7, but in dimension 8 my proof didn't work." So weird, but a common difficulty!
This is a month late but still worthy math fun. Stolen from MAA's fantastic Math Horizon magazine merely for educational purposes :)
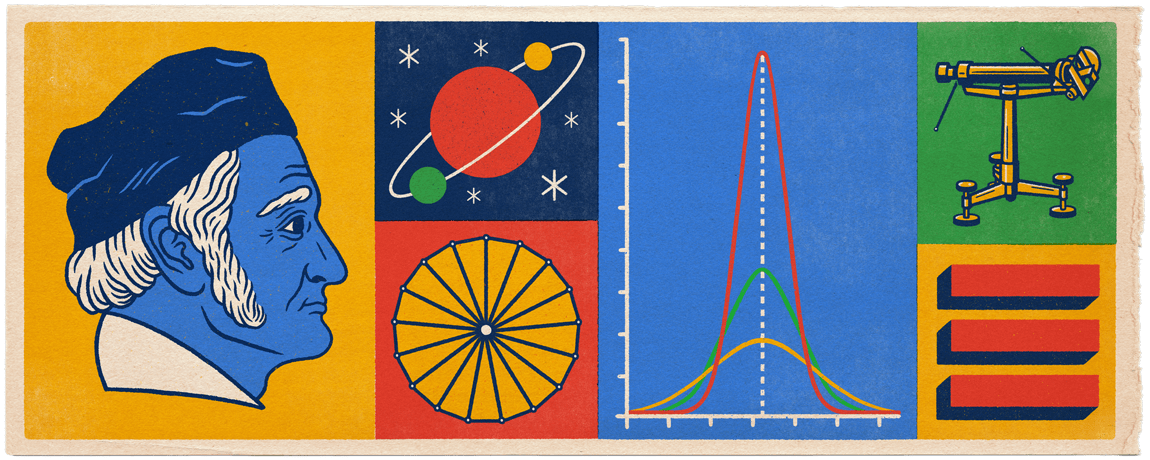
Happy anniversary of birth to Carl Friedrich Gauss, one of the most prolific mathematicians of all time (b. April 30, 1777).
A fun fact about Gauss is that he figured out a way to draw a 17-sided polygon using only a ruler and compass. "The proof rested on a profound analysis of the factorization of polynomial equations and opened the door to later ideas of Galois theory." (source: https://www.britannica.com/biography/Carl-Friedrich-Gauss image source: https://doodles.google/doodle/johann-carl-friedrich-gaus-241st-birthday/)
Attn Calc II students: This is a fun little integral. \( \int 2^{\ln(x)}dx \) A substitition \( u=\ln(x) \) won't work since there is no \( \frac{1}{x} \) to make the match. #integration #exponentiation
Think about before reading on.
Nifty trick! Since \( 2=e^{\ln(2)} \), then \( 2^{\ln(x)} = (e^{\ln(2)})^{\ln(x)}=(e^{\ln(x)})^{\ln(2)}=x^{\ln(2)} \)
Now the integral becomes \( \int x^{\ln(2)}dx = \frac{1}{1+ln(2)} x^{1+\ln(2)} + C \)
Swapping from an constant-to-variable to a variable-to-constant made a world of difference. Sweet!
Do you use your iPhone Calculator app for quick calculations? In case you didn't know, rotate your phone to landscape and it becomes a scientific calculator with radicals, exponentials, logarithms, trig functions, even hyperbolic trig functions.
Press "2nd" to get more functions including log-base-b, inverse trigs, inverse hyperbolic trigs.
One more hack: Entering numbers into the command line and mess up? No need to "C" clear all, just swipe right on the command line to delete the previous digit.
While DESMOS app and GeoGebra Apps are amazing for graphing, the built-in Calculator app on iPhone is handy! I keep it in my Control Center for easy access.
